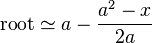Mental calculation comprises of Arithmetical calculations using only the Human brain with no help from calculators, computers, or pen and paper.
People use mental calculation when computing tools are not available,
when it is faster than other means of calculation (for example,
conventional methods as taught in educational institutions), or in a competitive context. Mental calculation often involves the use of specific techniques devised for specific types of problems.
Many of these techniques take advantage of or rely on the decimal numeral system. Usually, the choice of radix
determines what methods to use and also which calculations are easier
to perform mentally. For example, multiplying or dividing by ten is an
easy task when working in decimal (just move the decimal point), whereas
multiplying or dividing by sixteen is not; however, the opposite is
true when working in hexadecimal
mentawellbeing.blogspot.comAfter applying an arithmetic operation to two operands and getting a
result, you can use this procedure to improve your confidence that the
result is correct.
Sum the digits of the first operand; any 9s (or sets of digits that add to 9)can be counted as 0.
If the resulting sum has two or more digits, sum those digits as in
step one; repeat this step until the resulting sum has only one digit.
Repeat steps one and two with the second operand. You now have two
one-digit numbers, one condensed from the first operand and the other
condensed from the second operand. (These one-digit numbers are also the
remainders you would end up with if you divided the original operands
by 9; mathematically speaking, they're the original operands modulo 9.)
Apply the originally specified operation to the two condensed
operands, and then apply the summing-of-digits procedure to the result
of the operation.
Sum the digits of the result you originally obtained for the original calculation..
If the result of step 4 does not equal the result of step 5, then
the original answer is wrong. If the two results match, then the
original answer may be right, though it isn't guaranteed to be.
Example
Say we've calculated that 6338 × 79 equals 500702
Sum the digits of 6338: (6 + 3 = 9, so count that as 0) + 3 + 8 = 11
Iterate as needed: 1 + 1 =
2Sum the digits of 79: 7 + (9 counted as 0) =
7Perform the original operation on the condensed operands, and sum digits: 2 × 7 = 14; 1 + 4 =
5Sum the digits of 500702: 5 + 0 + 0 + (7 + 0 + 2 = 9, which counts as 0) =
55 = 5, so there's a good chance that we were right that 6338 × 79 equals 500702.
You can use the same procedure with multiple operations just repeat steps 1 and 2 for each operation.
Estimation
While checking the mental calculation, it is useful to think of it in
terms of scaling. For example, when dealing with large numbers, say
1531 × 19625, estimation instructs you to be aware of the number of
digits expected for the final value. A useful way of checking is to
estimate. 1531 is around 1500, and 19625 is around 20000, so a result of
around 20000 × 1500 (30000000) would be a good estimate for the actual
answer (30045875). So if the answer has too many digits, you know you've
made a mistake.
Factors
When multiplying, a useful thing to remember is that the factors of
the operands still remain. For example, to say that 14 × 15 was 211
would be unreasonable. Since 15 is a multiple of 5, the product should
be as well. Likewise, 14 is a multiple of 2, so the product should be
even. Furthermore, any number which is a multiple of both 5 and 2 is
necessarily a multiple of 10, and in the decimal system would end with a
0. The correct answer is 210. It is a multiple of 10, 7 (the other
prime factor of 14) and 3 (the other prime factor of 15).
Calculating differences: a − b
Direct calculation
When the digits of
b are all smaller than the corresponding digits of
a,
the calculation can be done digit by digit. For example, evaluate
872 − 41 simply by subtracting 1 from 2 in the units place, and 4 from 7
in the tens place: 831.
Indirect calculation
When the above situation does not apply, the problem can sometimes be modified:
If only one digit in
b is larger than its corresponding digit in
a, diminish the offending digit in
b until it is equal to its corresponding digit in
a. Then subtract further the amount
b was diminished by from
a. For example, to calculate 872 − 92, turn the problem into 872 − 72 = 800. Then subtract 20 from 800: 780.
If more than one digit in
b is larger than its corresponding digit in
a, it may be easier to find how much must be added to
b to get
a.
For example, to calculate 8192 − 732, we can add 8 to 732 (resulting in
740), then add 60 (to get 800), then 200 (for 1000). Next, add 192 to
arrive at 1192, and, finally, add 7000 to get 8192. Our final answer is
7460.
It might be easier to start from the left (the big numbers) first.
You may guess what is needed, and accumulate your guesses. Your guess
is good as long as you haven't gone beyond the "target" number.
8192 − 732, mentally, you want to add 8000 but that would be too much,
so we add 7000, then 700 to 1100, is 400 (so far we have 7400), and 32
to 92 can easily be recognized as 60. The result is 7460.
Look-ahead borrow method
This method can be used to subtract numbers left to right, and if all
that is required is to read the result aloud, it requires little of the
user's memory even to subtract numbers of arbitrary size.
One place at a time is handled, left to right.
Example:
4075
− 1844
------
Thousands: 4 − 1 = 3, look to right, 075 < 844, need to borrow.
3 − 1 = 2, say "Two thousand".
We are performing 3 - 1 rather than 4 - 1 because the column to the right is
going to borrow from the thousands place.
Hundreds: 0 − 8 = negative numbers not allowed here.
We are going to increase this place by using the number we borrowed from the
column to the left. Therefore:
10 − 8 = 2. It's 10 rather than 0, because we borrowed from the Thousands
place. 75 > 44 so no need to borrow,
say "two hundred"
Tens: 7 − 4 = 3, 5 > 4
Calculating products: a × b
Many of these methods work because of the distributive property
Multiplying by 2 or other small numbers
Where one number being multiplied is sufficiently small to be
multiplied with ease by any single digit, the product can be calculated
easily digit by digit from right to left. This is particularly easy for
multiplication by 2 since the carry digit cannot be more than 1.
For example, to calculate 2 × 167: 2×7=14, so the final digit is
4, with a 1 carried and added to the 2×6 = 12 to give 13, so the next digit is
3 with a 1 carried and added to the 2×1=2 to give
3. Thus, the product is 334.
Multiplying by 5
To multiply a number by 5,
1. First multiply that number by 10, then divide it by 2.
The following algorithm is a quick way to produce this result:
2. Add a zero to right side of the desired number. (A.) 3. Next,
starting from the leftmost numeral, divide by 2 (B.) and append each
result in the respective order to form a new number;(fraction answers
should be rounded down to the nearest whole number).
EXAMPLE: Multiply 176 by 5.
A. Add a zero to 176 to make 1760.
B. Divide by 2 starting at the left.
1. Divide 1 by 2 to get .5, rounded down to zero.
2. Divide 7 by 2 to get 3.5, rounded down to 3.
3. Divide 6 by 2 to get 3. Zero divided by two is simply zero.
The resulting number is 0330. (This is not the final answer, but a
first approximation which will be adjusted in the following step:)
C. Add 5 to the number that follows any single numeral
in this new number that was odd before dividing by two;
EXAMPLE: 176 (IN FIRST, SECOND THIRD PLACES):
1.The FIRST place is 1, which is odd. ADD 5 to the numeral after
the first place in our new number (0330) which is 3; 3+5=8.
2.The number in the second place of 176, 7, is also odd. The
corresponding number (0 8 3 0) is increased by 5 as well;
3+5=8.
3.The numeral in the third place of 176, 6, is even, therefore
the final number, zero, in our answer is not changed. That
final answer is 0880.
The leftmost zero can be omitted, leaving 880.
So 176 times 5 equals 880.
Multiplying by 9
Since 9 = 10 − 1, to multiply a number by nine, multiply it by 10 and
then subtract the original number from the result. For example, 9 × 27 =
270 − 27 = 243.
This method can be adjusted to multiply by eight instead of nine, by
doubling the number being subtracted; 8 × 27 = 270 − (2×27) = 270 − 54 =
216.
Similarly, by adding instead of subtracting, the same methods can be
used to multiply by 11 and 12, respectively (although simpler methods to
multiply by 11 exist).
Using hands: 1–10 multiplied by 9
Hold hands in front of you, palms facing you. Assign the left thumb
to be 1, the left index to be 2, and so on all the way to right thumb is
ten. Each "|" symbolizes a raised finger and a "−" represents a bent
finger.
1 2 3 4 5 6 7 8 9 10
| | | | | | | | | |
left hand right hand
Bend the finger which represents the number to be multiplied by nine down.
Ex: 6 × 9 would be
| | | | | − | | | |
The right little finger is down. Take the number of fingers still
raised to the left of the bent finger and prepend it to the number of
fingers to the right.
Ex: There are five fingers left of the right little finger and four to the right of the right little finger. So 6 × 9 = 54.
5 4
| | | | | − | | | |
Multiplying by 10 (and powers of ten)
To multiply an integer by 10, simply add an extra 0 to the end of the
number. To multiply a non-integer by 10, move the decimal point to the
right one digit.
In general for base ten, to multiply by 10
n (where
n is an integer), move the decimal point
n digits to the right. If
n is negative, move the decimal |
n| digits to the left.
Multiplying by 11
For single digit numbers simply duplicate the number into the tens
digit, for example: 1 × 11 = 11, 2 × 11 = 22, up to 9 × 11 = 99.
The product for any larger non-zero Integer can be found by a series of additions to each of its digits from right to left, two at a time.
First take the ones digit and copy that to the temporary result.
Next, starting with the ones digit of the multiplier, add each digit to
the digit to its left. Each sum is then added to the left of the result,
in front of all others. If a number sums to 10 or higher take the tens
digit, which will always be 1, and carry it over to the next addition.
Finally copy the multipliers left-most (highest valued) digit to the
front of the result, adding in the carried 1 if necessary, to get the
final product.
In the case of a negative 11, multiplier, or both apply the sign to
the final product as per normal multiplication of the two numbers.
A step-by-step example of 759 × 11:
The ones digit of the multiplier, 9, is copied to the temporary result.
result: 9
Add 5 + 9 = 14 so 4 is placed on the left side of the result and carry the 1.
result: 49
Similarly add 7 + 5 = 12, then add the carried 1 to get 13. Place 3 to the result and carry the 1.
result: 349
Add the carried 1 to the highest valued digit in the multiplier, 7 + 1 = 8, and copy to the result to finish.
Final product of 759 × 11: 8349
Further examples:
−54 × −11 = 5 5+4(9) 4 = 594
999 × 11 = 9+1(10) 9+9+1(9) 9+9(8) 9 = 10989
Note the handling of 9+1 as the highest valued digit.
−3478 × 11 = 3 3+4+1(8) 4+7+1(2) 7+8(5) 8 = −38258
62473 × 11 = 6 6+2(8) 2+4+1(7) 4+7+1(2) 7+3(0) 3 = 687203
Another method is to simply multiply the number by 10, and add the original number to the result.
For example:
17 × 11
17 × 10 = 170
170 + 17 = 187
17 × 11 = 187
One last easy way:
If you have a two-digit number, take it and add the two numbers
together and put that sum in the middle, and you can get the answer.
For example: 24 x 11 = 264 because 2 + 4 = 6 and the 6 is placed in between the 2 and the 4.
Second example: 87 x 11 = 957 because 8 + 7 = 15 so the 5 goes in
between the 8 and the 7 and the 1 is carried to the 8. So it is
basically 857 + 100 = 957.
Or if 43 x 11 is equal to first 4+3=7 (For the tens digit) Then 4 is
for the hundreds and 3 is for the tens. And the answer is 473
Multiplying two 2 digit numbers between 11 and 19
To easily multiply 2 digit numbers together between 11 and 19 a
simple algorithm is as follows (where a is the ones digit of the first
number and b is the ones digit of the second number):
(10+a)×(10+b)
100 + 10×(a+b) + a×b
which can be visualized as three parts to be added:
1
xx
yy
for example:
17×16
1 = 100
13 (7+6) = 10×(a+b)
42 (7×6) = a×b
272 (total)
Multiplying any 2-digit numbers
To easily multiply any 2-digit numbers together a simple algorithm is
as follows (where a is the tens digit of the first number, b is the
ones digit of the first number, c is the tens digit of the second number
and d is the ones digit of the second number):


For example

800
+120
+140
+ 21
-----
1081
Note that this is the same thing as the conventional sum of partial
products, just restated with brevity. To minimize the number of elements
being retained in one's memory, it may be convenient to perform the sum
of the "cross" multiplication product first, and then add the other two
elements:


[of which only the tens digit will interfere with the first term]

i.e., in this example
(12 + 14) = 26, 26 × 10 = 260,
to which is it is easy to add 21: 281 and then 800: 1081
An easy mnemonic to remember for this would be FOIL. F meaning first, O meaning outer, I meaning inner and L meaning last. For example:

and

where 7 is
a, 5 is
b, 2 is
c and 3 is
d.
Consider
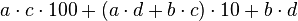
this expression is analogous to any number in base 10 with a
hundreds, tens and ones place. FOIL can also be looked at as a number
with F being the hundreds, OI being the tens and L being the ones.
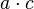
is the product of the first digit of each of the two numbers; F.
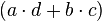
is the addition of the product of the outer digits and the inner digits; OI.

is the product of the last digit of each of the two numbers; L.
Multiplying any two numbers by attaching, subtracting, and routing
Discovered by Artem Cheprasov, there is a method of multiplication
that allows the user to utilize 3 steps to quickly multiply numbers of
any size to one another via three unique ways.
First, the method allows the user to attach numbers to one another,
as opposed to adding or subtracting them, during intermediate steps in
order to quicken the rate of multiplication. For instance, instead of
adding or subtracting intermediary results such as 357 and 84, the user
could simply attach the numbers together (35784) in order to simplify
and expedite the multiplication problem. Attaching numbers to one
another helps to bypass unnecessary steps found in traditional
multiplication techniques.
Secondly, this method uses negative numbers as necessary, even when
multiplying two positive integers, in order to quicken the rate of
multiplication via subtraction. This means two positive integers can be
multiplied together to get negative intermediate steps, yet still the
correct positive answer in the end. These negative numbers are actually
automatically derived from the multiplication steps themselves and are
thus unique to a particular problem. Again, such negative intermediate
steps are designed to help hasten the mental math.
Finally, another unique aspect of using this method is that the user
is able to choose one of several different “routes of multiplication” to
the specific multiplication problem at hand based on their subjective
preferences or strengths and weaknesses with particular integers.
Despite the same starting integers, the different multiplication
routes give off different intermediate numbers that are automatically
derived for the user as they multiply. Some of these intermediaries may
be easier than others (e.g. some users may find a route that uses a
negative 7, while another route uses a 5 or a 0, which are typically
easier to work with mentally for most people, but not in all instances).
If one “route” seems to be harder for one student vs. another route
and its intermediate numbers, that student can simply choose another
simpler route of multiplication for themselves even though it’s the same
original problem.
The "Ends of Five" Formula
For any 2 digit by 2 digit multiplication problem, if both numbers
end in five, the following algorithm can be used to quickly multiply
them together:

As a preliminary step simply round the smaller number down and the larger up to the nearest multiple of ten. In this case:


The algorithm reads as follows:

Where t
1 is the tens unit of the original larger number (75) and t
2 is the tens unit of the original smaller number (35).

The author also outlines another similar algorithm if you want to
round the original larger number down and the original smaller number up
instead.
The "Borrower's" Formula
If two numbers are equidistant from the nearest multiple of 100, then a simple algorithm can be used to find the product.
As a simple example:

Both numbers are equidistant (33 away) from their nearest multiple of 100 (0 and 100, respectively).
As a preliminary step simply round the smaller number down and the larger up to the nearest multiple of ten. In this case:


The algorithm reads as follows:

Where u
1 is the original larger number's (67) units digit and u
2 is the original smaller number's (33) units digit. T
1 is the original larger number's tens digit and T
2 is the original larger number's tens digit multiplied by their respective power (in this case by 10, for a tens digit).
And so:

Using hands: 6–10 multiplied by another number 6–10
This technique allows a number from 6 to 10 to be multiplied by another number from 6 to 10.
Assign 6 to the little finger, 7 to the ring finger, 8 to the middle
finger, 9 to the index finger, and 10 to the thumb. Touch the two
desired numbers together. The point of contact and below is considered
the "bottom" section and everything above the two fingers that are
touching are part of the "top" section. The answer is formed by adding
ten times the total number of "bottom" fingers to the product of the
number of left- and right-hand "top" fingers.
For example, 9 × 6 would look like this, with the left index finger touching the right little finger:
=10== :right thumb (top)
==9== :right index finger (top)
==8== :right middle finger (top)
left thumb: =10== ==7== :right ring finger (top)
left index finger: --9---><---6-- :right little finger (BOTTOM)
left middle finger: --8-- (BOTTOM)
left ring finger: --7-- (BOTTOM)
left little finger: --6-- (BOTTOM)
In this example, there are 5 "bottom" fingers (the left index,
middle, ring, and little fingers, plus the right little finger), 1 left
"top" finger (the left thumb), and 4 right "top" fingers (the right
thumb, index finger, middle finger, and ring finger). So the computation
goes as follows: 9 × 6 = (10 × 5) + (1 × 4) = 54.
Consider another example, 8 × 7:
=10== :right thumb (top)
left thumb: =10== ==9== :right index finger (top)
left index finger: ==9== ==8== :right middle finger (top)
left middle finger: --8---><---7-- :right ring finger (BOTTOM)
left ring finger: --7-- --6-- :right little finger (BOTTOM)
left little finger: --6-- (BOTTOM)
Five bottom fingers make 5 tens, or 50. Two top left fingers and
three top right fingers make the product 6. Summing these produces the
answer, 56.
Another example, this time using 6 × 8:
--8---><---6--
--7--
--6--
Four tens (bottom), plus two times four (top) gives 40 + 2 × 4 = 48.
Here's how it works: each finger represents a number between 6 and 10. When you join fingers representing
x and
y, there will be 10 -
x "top" fingers and
x - 5 "bottom" fingers on the left hand; the right hand will have 10 -
y "top" fingers and
y - 5 "bottom" fingers.
Let
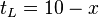
(the number of "top" fingers on the left hand)

(the number of "top" fingers on the right hand)

(the number of "bottom" fingers on the left hand)

(the number of "bottom" fingers on the right hand)
Then following the above instructions produces
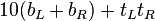
![\, =10[(x-5)+(y-5)] + (10-x)(10-y)](https://upload.wikimedia.org/math/b/5/0/b506130b3f17c087d32cff3bf4889e12.png)

![\, =[10(x+y) - 100] + [100 - 10(x+y) + xy]](https://upload.wikimedia.org/math/5/d/e/5de767bc2b44cf2ea9b03dc6829ffc49.png)
![\, =[10(x+y)-10(x+y)] + [100-100] + xy](https://upload.wikimedia.org/math/6/0/1/60186e041fe6b8980c94964fd4c05754.png)

which is the product we seek.
Multiplying two numbers close and below 100
This technique allows easy multiplication of numbers close and below 100.(90-99)
[3] The variables will be the two numbers you multiply.
The product of two variables ranging from 90-99 will result in a
4-digit number. The first step is to find the ones-digit and the tens
digit.
Subtract both variables from 100 which will result in 2 one-digit
number. The product of the 2 one-digit numbers will be the last two
digits of your final product.
Next, subtract one of the two variables from 100. Then subtract the
difference from the other variable. That difference will be the first
two digits of your final product. And the resulting 4 digit number will
be the final product.
Example:
95
x 97
----
Last two digits: 100-95=5 (subtract first number from 100)
100-97=3 (subtract second number from 100)
5*3=15 (multiply the two differences)
Final Product- yx15
First two digits: 100-95=5 (Subtract the first number of your equation from 100)
97-5=92 (Subtract that answer from the second number of your equation)
Now, the difference will be the first two digits
Final Product- 9215
Alternate for first two digits
5+3=8 (Add the two single digits derived when calculating "Last two digits" in previous step)
100-8=92 (Subtract that answer from 100)
Now, the difference will be the first two digits
Final Product- 9215
Using square numbers
The products of small numbers may be calculated by using the squares
of integers; for example, to calculate 13 × 17, you can remark 15 is the
mean of the two factors, and think of it as (15 − 2) × (15 + 2),
i.e. 15² − 2². Knowing that 15² is 225 and 2² is 4, simple subtraction shows that 225 − 4 = 221, which is the desired product.
This method requires knowing by heart a certain number of squares:
| 12 = 1 |
62 = 36 |
112 = 121 |
162 = 256 |
212 = 441 |
262 = 676 |
| 22 = 4 |
72 = 49 |
122 = 144 |
172 = 289 |
222 = 484 |
272 = 729 |
| 32 = 9 |
82 = 64 |
132 = 169 |
182 = 324 |
232 = 529 |
282 = 784 |
| 42 = 16 |
92 = 81 |
142 = 196 |
192 = 361 |
242 = 576 |
292 = 841 |
| 52 = 25 |
102 = 100 |
152 = 225 |
202 = 400 |
252 = 625 |
302 = 900 |
Squaring numbers
It may be useful to be aware that the difference between two
successive square numbers is the sum of their respective square roots.
Hence if you know that 12 × 12 = 144 and wish to know 13 × 13, calculate
144 + 12 + 13 = 169.
This is because (
x + 1)
2 −
x2 =
x2 + 2
x + 1 −
x2 =
x + (
x + 1)
x2 = (
x − 1)
2 + (2
x − 1)
Squaring numbers near 50
Suppose we need to square a number
x near 50. This number may be expressed as
x = 50 −
n, and hence the answer
x2 is (50−
n)
2, which is 50
2 − 100n +
n2. We know that 50
2 is 2500. So we subtract 100
n from 2500, and then add
n2. Example, say we want to square 48, which is 50 − 2. We subtract 200 from 2500 and add 4, and get
x2 = 2304. For numbers larger than 50 (
x = 50 +
n), add
n a hundred times instead of subtracting it.
Squaring a number ending in 5
Take the digit(s) that precede the five:
abc5, where
a, b, and
c are digits
Multiply this number by itself plus one:
abc(
abc + 1)
Take above result and attach
25 to the end
Example: 85 × 85
- 8
- 8 × 9 = 72
- So, 852 = 7,225
Example: 125
2
- 12
- 12 × 13 = 156
- So, 1252 = 15,625
Mathematical explanation
| (10x + 5)2 |
= (10x + 5)(10x + 5) |
|
= 100x2 + 100x + 25 |
|
= 100(x2 + x) + 25 |
|
= 100x(x + 1) + 25 |
Squaring an integer from 26 to 75
This method requires the memorization of squares from 1 to 25.
The square of
n (most easily calculated when
n is between 26 and 75 inclusive) is
(50 −
n)
2 + 100(
n − 25)
In other words, the square of a number is the square of its
difference from fifty added to one hundred times the difference of the
number and twenty five. For example, to square 62, we have:
(−12)
2 + [(62-25) × 100]
= 144 + 3,700
= 3,844
Squaring an integer from 76 to 125
This method requires the memorization of squares from 1 to 25.
The square of
n (most easily calculated when
n is between 76 and 125 inclusive) is
(100 −
n)
2 + 100(100 − 2(100 −
n))
In other words, the square of a number is the square of its
difference from one hundred added to the product of one hundred and the
difference of one hundred and the product of two and the difference of
one hundred and the number. For example, to square 93, we have:
7
2 + 100(100 − 2(7))
= 49 + 100 × 86
= 49 + 8,600
= 8,649
Another way to look at it would be like this:
93
2 = ? (is −7 from 100)
93 − 7 = 86 (this gives us our first two digits)
(−7)
2 = 49 (these are the second two digits)
93
2 = 8649
Another example:
822 = ? (is −18 from 100)
82 − 18 = 64 (subtract. First digits.)
(−18)2 = 324 (second pair of digits. We'll need to carry the 3.)
82² = 6724
Squaring any number
Take a given number, and add and subtract a certain value to it that will make it easier to multiply. For example:
492
2
492 is close to 500, which is easy to multiply by. Add and subtract 8 (the difference between 500 and 492) to get
492 -> 484, 500
Multiply these numbers together to get 242,000 (This can be done
efficiently by dividing 484 by 2 = 242 and multiplying by 1000).
Finally, add the difference (8) squared (8
2 = 64) to the result:
492
2 = 242,064
The proof follows:




Squaring any 2-digit integers
This method requires memorization of the squares of the one-digit numbers 1 to 9.
The square of
mn,
mn being a two-digit integer, can be calculated as
10 ×
m(
mn +
n) +
n2
Meaning the square of
mn can be found by adding
n to
mn, multiplied by
m, adding 0 to the end and finally adding the square of
n.
For example, we have 23
2:
23
2= 10 × 2(23 + 3) + 3
2= 10 × 2(26) + 9
= 520 + 9
= 529
So 23
2 = 529.
Finding roots
Approximating square roots
An easy way to approximate the
square root of a number is to use the following equation:

The closer the known square
is to the unknown, the more accurate the approximation. For instance,
to estimate the square root of 15, we could start with the knowledge
that the nearest perfect square is 16 (4
2).

So we've estimated the square root of 15 to be 3.875. The actual square root of 15 is 3.872983...
Derivation
Say we want to find the square root of a number we'll call x. By definition

We then redefine the root

where a is a known root (4 from the above example) and b is the difference between the known root and the answer we seek.

Expanding yields

And here's the trick. If 'a' is close to your target, 'b' will be a small enough number to render the

element of the equation negligible. So we drop

out and rearrange the equation to

and therefore
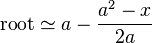
that can be reduced to

Extracting roots of perfect powers
is often practiced. The difficulty of the task does not depend on the
number of digits of the perfect power but on the precision, i.e. the
number of digits of the root.
An easy task for the beginner is extracting cube roots from the cubes
of 2 digit numbers. For example, given 74088, determine what two digit
number, when multiplied by itself once and then multiplied by the number
again, yields 74088. One who knows the method will quickly know the
answer is 42, as 423 = 74088.
Before learning the procedure, it is required that the performer memorize the cubes of the numbers 1-10:
| 13 = 1 |
23 = 8 |
33 = 27 |
43 = 64 |
53 = 125 |
| 63 = 216 |
73 = 343 |
83 = 512 |
93 = 729 |
103 = 1000 |
Observe that there is a pattern in the rightmost digit: adding and subtracting with 1 or 3. Starting from zero:
- 03 = 0
- 13 = 1 up 1
- 23 = 8 down 3
- 33 = 27 down 1
- 43 = 64 down 3
- 53 = 125 up 1
- 63 = 216 up 1
- 73 = 343 down 3
- 83 = 512 down 1
- 93 = 729 down 3
- 103 = 1000 up 1
There are two steps to extracting the cube root from the cube of a
two digit number. Say you are asked to extract the cube root of 29791.
Begin by determining the one's place (units) of the two digit number.
You know it must be one, since the cube ends in 1, as seen above.
- If perfect cube ends in 0, the cube root of it must end in 0.
- If perfect cube ends in 1, the cube root of it must end in 1.
- If perfect cube ends in 2, the cube root of it must end in 8.
- If perfect cube ends in 3, the cube root of it must end in 7.
- If perfect cube ends in 4, the cube root of it must end in 4.
- If perfect cube ends in 5, the cube root of it must end in 5.
- If perfect cube ends in 6, the cube root of it must end in 6.
- If perfect cube ends in 7, the cube root of it must end in 3.
- If perfect cube ends in 8, the cube root of it must end in 2.
- If perfect cube ends in 9, the cube root of it must end in 9.
Note that every digit corresponds to itself except for 2, 3, 7 and 8,
which are just subtracted from ten to obtain the corresponding digit.
The second step is to determine the first digit of the two digit cube
root by looking at the magnitude of the given cube. To do this, remove
the last three digits of the given cube (29791 → 29) and find the
greatest cube it is greater than (this is where knowing the cubes of
numbers 1-10 is needed). Here, 29 is greater than 1 cubed, greater than 2
cubed, greater than 3 cubed, but not greater than 4 cubed. The greatest
cube it is greater than is 3, so the first digit of the two digit cube
must be 3.
Therefore, the cube root of 29791 is 31.
Another example:
- Find the cube root of 456533.
- The cube root ends in 7.
- After the last three digits are taken away, 456 remains.
- 456 is greater than all the cubes up to 7 cubed.
- The first digit of the cube root is 7.
- The cube root of 456533 is 77.
This process can be extended to find cube roots that are 3 digits long, by using arithmetic modulo 11.
Approximating common logs (log base 10)
To approximate a common log (to at least one decimal point accuracy),
a few log rules, and the memorization of a few logs is required. One
must know:
- log(a x b) = log(a) + log(b)
- log(a / b) = log(a) - log(b)
- log(0) does not exist
- log(1) = 0
- log(2) ~ .30
- log(3) ~ .48
- log(7) ~ .85
From this information, one can find the log of any number 1-9.
- log(1) = 0
- log(2) ~ .30
- log(3) ~ .48
- log(4) = log(2 × 2) = log(2) + log(2) ~ .60
- log(5) = log(10 / 2) = log(10) − log(2) ~ .70
- log(6) = log(2 × 3) = log(2) + log(3) ~ .78
- log(7) ~ .85
- log(8) = log(2 × 2 × 2) = log(2) + log(2) + log(2) ~ .90
- log(9) = log(3 × 3) = log(3) + log(3) ~ .96
- log(10) = 1 + log(1) = 1
The first step in approximating the common log is to put the number
given in scientific notation. For example, the number 45 in scientific
notation is 4.5 x 10^1, but we will call it a x 10^b. Next, find the log
of a, which is between 1 and 10. Start by finding the log of 4, which
is .60, and then the log of 5, which is .70 because 4.5 is between these
two. Next, and skill at this comes with practice, place a 5 on a
logarithmic scale between .6 and .7, somewhere around .653 (NOTE: the
actual value of the extra places will always be greater than if it were
placed on a regular scale. i.e., you would expect it to go at .650
because it is halfway, but instead it will be a little larger, in this
case .653) Once you have obtained the log of a, simply add b to it to
get the approximation of the common log. In this case, a + b = .653 + 1 =
1.653. The actual value of log(45) ~ 1.65321.
The same process applies for numbers between 0 and 1. For example, 0.045 would be written as 4.5 × 10−2.
The only difference is that b is now negative, so when adding you are
really subtracting. This would yield the result 0.653 − 2, or −1.347.
Approximating natural exponents (log base e)
Natural exponents are used in many important expressions in modern
science and engineering, with applications not limited to quantum
mechanics, thermodynamics and signal communications. Using the laws of
Natural exponents, memorization of the approximations below, and
combination with other mental calculation methods, create a powerful and
elegant means for changing complicated problems in the physical
sciences into simple sums and products. The laws of Natural exponents (Exponentiation) are:
- ea x eb = e (a+b) and e −a = 1/ ea and also
- ea x e−b = e (a-b) = ea / eb
Table of approximations
Where possible, single digit numbers, followed by zeros, are used for
ease of memorization, accuracy and to eliminate redundancy: (e4.5)2 = e9, e3 x e4 = e7, and e8 are used instead of (e4)2.
| Exponent |
Value |
Error |
|
Exponent |
Value |
Error |
| e3 |
≈ 20 |
0.43%+ |
|
e23 |
≈ 1010 |
0.11%+ |
| e4 |
≈ 55 |
0.74%− |
|
e25 |
≈ 7.2x1010 |
0.0003%+ |
| e4.25 |
≈ 70 |
0.15%− |
|
e50.6 |
≈ 1022 |
0.02%+ |
| e4.5 |
≈ 90 |
0.02%− |
|
e61 |
≈ π x 1026 |
0.02%− |
| e5.75 |
≈ 100π |
0.01%− |
|
e99 |
≈ 1043 |
0.01%− |
| e8 |
≈ 3,000 |
0.64%− |
|
e108 |
≈ 8x1046 |
0.0015%− |
Optimized Relations
This table presents optimized suggestions derived from the above table.
| e10 |
= e3x e7 |
≈ 22,000 |
0.01%+ |
|
e0.25 |
= e4.25 /e4 |
≈ 70/55 |
3.5%+ |
| e1 |
= e10 /e9 |
≈ 220/81 |
0.08%+ |
|
e0.5 |
= e4.5 /e4 |
≈ 90/55 |
1.5%+ |
| e2 |
= e9 / e7 |
≈ 81/11 |
0.4%− |
|
e0.3 |
= √(e50.6) /e25 = e25.3 /e25 |
≈ 100/72 |
0.5%+ |
| e5 |
= e9 /e4 |
≈ 8100/55 |
0.15%− |
|
|
better approximations: |
e4 ≈ 54.6 |
e6 ≈ 403 or 404 |
Physical Science and Communication Approximations
| Exponent |
Value |
Error |
Application |
| eπ |
≈ 20+π |
0.004%− |
Spherical wave attenuation |
| e274 |
≈ 10119 |
0.0003%+ |
1 °C, 274 Kelvin |
| e280 |
≈ 4 x 10121 |
0.00003%+ |
e280/e7 = e273 near ambient, Kelvin |
| e452 |
≈ 2 x 10196 |
0.000004%+ |
Accurate thermal temperature |
| kbe2 |
≈ 10−22 |
1.4%+ |
kb = Boltzmann's constant |
The +/- superscript after the error represents if the actual number
value is higher or lower than the approximation; for example the
approximation of ln(400) is less than 6. The +/- symbols after errors
may also be used to make the approximations more accurate by
compensation, for example;
- e16 = e8 x e8, accurate to 12 parts in 1000, may be made more accurate by using
- e7 x e9 ≈ 1,100 x 8,100 or 8,910,000, accuracy 2 parts in 1000.
Other examples
- e(9 + π) = 8,100 x (20 + π) = 162,000 + ~25,500 = 187,500, (accurate to 1 part in 5000)
Mental arithmetic as a psychological skill
Physical assertion of the proper level can lead to an increase in performance of a mental task, like doing mental calculations, performed afterward. It has been shown that during high levels of physical activity there is a negative effect on mental task performance. This means that too much physical work can decrease accuracy and output of mental math calculations. Physiological measures, specifically EEG, have been shown to be useful in indicating Mental workload Using an EEG as a measure of mental workload after different levels of
physical activity can help determine the level of physical exertion that
will be the most beneficial to mental performance. Previous work done
at
Michigan Technological University by Ranjana Mehta includes a recent study that involved participants engaging in concurrent mental and physical tasks.
This study investigated the effects of mental demands on physical
performance at different levels of physical exertion and ultimately
found a decrease in physical performance when mental tasks were
completed concurrently, with a more
significant effect at the higher level of physical workload. The
Brown-Peterson procedure is a widely known task using mental arithmetic. This procedure, mostly used in
cognitive experiments, suggests mental subtraction is useful in testing the effects
maintenance rehearsal can have on how long
short-term memory lasts.
Mental Calculations World Championship
The first Mental Calculations World Championship took place in 1997 at the
Mind Sports Olympiad.
This event repeats every year. It consists of a range of different
tasks such as: addition of ten ten-digit numbers, multiplication of two
eight-digit numbers, calculation of square roots, and calculation of
weekdays for given dates, calculation of cube roots plus some surprise
miscellaneous tasks.
Mental Calculation World Cup
The first World Mental Calculation Championships (
Mental Calculation World Cup)
took place in 2004. They are repeated every second year. It consists of
six different tasks: addition of ten ten-digit numbers, multiplication
of two eight-digit numbers, calculation of square roots, and calculation
of weekdays for given dates, calculation of cube roots plus some
surprise miscellaneous tasks.
Memoriad - World Memory, Mental Calculation & Speed Reading Olympics
Memoriad is the first platform combining "mental calculation", "memory" and
"photographic reading" competitions. Games and competitions are held in
the year of the Olympic games, every four years. The first Memoriad was
held in
Istanbul,
Turkey, in 2008. The second Memoriad took place in
Antalya,
Turkey
on 24–25 November 2012. 89 competitors from 20 countries participated.
Awards and money prizes were given for 10 categories in total; of which 5
categories had to do about mental calculation (Mental addition, Mental Multiplication, Mental Square Roots (non-integer), Mental Calendar Dates calculation and Flash Anzan).
Sourced: Wikipedia(2016).







 [of which only the tens digit will interfere with the first term]
[of which only the tens digit will interfere with the first term]


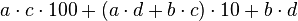
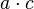 is the product of the first digit of each of the two numbers; F.
is the product of the first digit of each of the two numbers; F.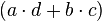 is the addition of the product of the outer digits and the inner digits; OI.
is the addition of the product of the outer digits and the inner digits; OI. is the product of the last digit of each of the two numbers; L.
is the product of the last digit of each of the two numbers; L.









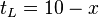 (the number of "top" fingers on the left hand)
(the number of "top" fingers on the left hand) (the number of "top" fingers on the right hand)
(the number of "top" fingers on the right hand) (the number of "bottom" fingers on the left hand)
(the number of "bottom" fingers on the left hand) (the number of "bottom" fingers on the right hand)
(the number of "bottom" fingers on the right hand)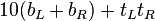
![\, =10[(x-5)+(y-5)] + (10-x)(10-y)](https://upload.wikimedia.org/math/b/5/0/b506130b3f17c087d32cff3bf4889e12.png)

![\, =[10(x+y) - 100] + [100 - 10(x+y) + xy]](https://upload.wikimedia.org/math/5/d/e/5de767bc2b44cf2ea9b03dc6829ffc49.png)
![\, =[10(x+y)-10(x+y)] + [100-100] + xy](https://upload.wikimedia.org/math/6/0/1/60186e041fe6b8980c94964fd4c05754.png)











 element of the equation negligible. So we drop
element of the equation negligible. So we drop